This article in english.
[Ed.-Notiz: Dennis Schulmeister ist ein Gymnasiast, der zur Zeit in Deutschland lernt. (per 2005)]
Ein Tontechniker sollte wenigstens ein bisschen über die Physik von Wellen verstehen. Unabhängig davon, ob es gilt ein Live-Konzert zu bestreiten, die Mikros im Studio aufgestellt werden müssen, oder gar ein Raum akustisch behandelt werden soll, es gibt eine Hand voll Richtlinien und Regeln, welche bei ordnungsgemäßem Einsatz einem das Leben um einiges leichter machen können.
Jeder Klang wird aus Wellen zusammengesetzt doch bevor darauf genauer eingehen lass uns erst einmal über Oszillationen sprechen. Wir werden nicht lange brauchen, da die meisten Gesetze der Oszillationen nur wenig Praxisbezug für uns haben aber schauen wir mal, wie das so von statten geht.
Im täglichen Leben begegnen uns in der Tat einige Oszillatoren (oder Schwinger, wie man will): Stimmgabeln, Gitarrensaiten, Saiten überhaupt, Verstärkerrückkopplung, Federn und so weiter. All diese Schwinger können verschiedenen Gruppen zugewiesen werden. Wir unterscheiden dabei zwischen harmonischen und unharmonischen Oszillatoren oder zwischen freien und gezwungenen Schwingern.
Ja was ist denn nun ein freier Schwinger? Eine freier Schwinger ist so zu sagen alles, was die Möglichkeit besitzt, zu vibrieren. Freie Oszillatoren sind zum Beispiel die Stimmgabel, die Saiten oder die Federn. Ein Beispiel für einen gezwungenen Oszillator ist ein üblicher Lautsprecher. Freie Oszillatoren leiten ihre Schwingungseigenschaften von ihrem Aufbau ab. Einmal angeregt, schwingen sie so lange, bis die dazu aufgewandte Energie komplett aufgebraucht wurde. Ein Lautsprecher vibriert nicht von alleine, er muss angeregt werden. (Meistens durch Verstärker.) Andauernde Kräfte werden müssen auf den Lautsprecher übertragen werden, andernfalls täte er gar nichts. Dafür liegen verschiedene Schwingungsgeschwindigkeiten in seiner Natur.
Nachdem wir nun freie und gezwungene Schwinger definiert haben, bleibt natürlich die Frage was das alles bedeutet. Im Gegensatz zu Gitarrensaiten schwingt eine Stimmgabel sehr symmetrisch. Eine gute Stimmgabel produziert dabei nur exakt eine Frequenz (z.B. 440 Hz). Das liegt daran, dass den Zungen der Stimmgabel eine Masse sowie eine gewisse Elastizität zugeordnet werden kann. Die Lage der Zungen bevor Energie zugeführt wurden nennt man Ruhelage. Die Auslenkung ist proportional zur Stärke der zugeführten Kraft. Das heißt, je stärker man die Gabel anstößt, desto größer ist die Auslenkung. Hier greift Newtons erstes Gesetz: Ein Körper verbleibt in Ruhelage oder einer gleichmäßigen Bewegung bis eine andere Kraft dem entgegen wirkt. Auf Grund der ständigen Interaktion der beiden gegenseitigen Kräfte Elastizität und Trägheit bewegen sich die Zungen kontinuierlich vor und zurück, sprich sie vibrieren.
Gitarrensaiten haben einen reicheres Klangbild und produzieren nicht nur exakt eine Frequenz gleichzeitig. Das heißt, sie sind unharmonische Schwinger.
In der Physik verwendet man gerne Spiralfedern, da sie langsam genug schwingen, um mit dem bloßen Auge beobachtet zu werden. Ein kleines Experiment soll die harmonischen Schwinger vertiefen:
Akustik 1.1
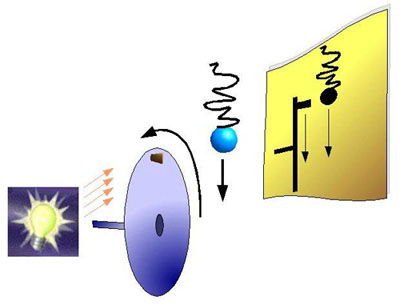
Auf dem Bild sehen wir eine Lichtquelle, eine dahinter befindliche Drehscheibe, auf der ein Korken angebracht wurde, als auch eine Spiralfeder mit einem Kügelchen und einem Blatt Papier, das als Schirm dient, in einer Reihe angeordnet. Zunächst ziehen wir ein wenig an der Feder so, dass sie anfängt zu schwingen. Dann probieren wir die Drehgeschwindigkeit der Scheibe so anzugleichen, dass sich beide Schatten auf dem Schirm gleichzeitig auf und ab bewegen. Ist das möglich? Ja, es IST möglich, die Geschwindigkeit der Scheibe so fest zu legen, dass sich sie Schatten gemeinsam bewegen. Eine (langweilige) Mathematik später und wir können schon die Position der Feder zu einer gegebenen Zeit berechnen*.
s = ^s * sin(w*t)
wobei ^s die größtmögliche Auslenkung der Feder, w die Winkelgeschwindigkeit und t die Zeit in Sekunden ist. Die Winkelgeschwindigkeit w ist wie folgt festgelegt:
w = 2pi*f
f ist dabei die Frequenz in Hz (Bewegungen pro Sekunde) und pi die Kreiszahl pi also ungefähr
3,14159.
Na toll. Und was haben wir nun daraus gelernt? Es gibt verschiedene Arten von Schwingungen. Freie und erzwungene Schwingungen, harmonische und unharmonische Schwingungen. Im Gegensatz zu den erzwungenen Schwingungen muss freien Schwingern nicht kontinuierlich Kraft übertragen werden, um sie am Schwingen zu erhalten. (Von der Reibung abgesehen, welche dem entgegen wirkt.)
Unharmonische Schwinger besitzen keine Fixfrequenz und schwingen nicht gleichmäßig. Die Position eines harmonischen Schwingers zu einer gegebenen Zeit t mit einer
gegebenen Frequenz f kann wie folgt errechnet werden:
s(f,t) = ^s * sin(2*pi*f*t)
^s ist wieder eine der Extrempositionen. Aber was bedeutet diese Mathematik nun für uns? Lass mich dir ein weiteres Schaubild zeigen. Wie würde die s(f,t)-Funktion ausschauen, wenn man sie in ein Koordinatensystem einzeichnete?
Akustik 1.2
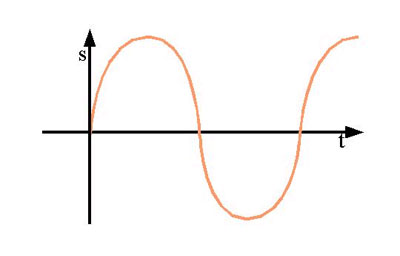
Merke: Der Pfeil, der nach oben zeigt ist die y-Achse, also die Auslenkung in unserem Fall. Der horizontale Pfeil ist die x-Achse. Die Kurve ist eigentlich aus vielen Punkten zusammengesetzt, die entlang beider Achsen verteilt werden.
Die x-Koordinate gibt üblicher weiße die Zeit an. Die y-Koordinate repräsentiert die Höhe auf der die Feder (bzw. die Kugel, die an ihr hängt) gerade ist. Schaut man der Feder eine weile zu, wird man fest stellen, dass die Kugel regelmäßig hoch und runter hüpft, manchmal etwas schneller, manchmal etwas langsamer. Und das ist auch alles, worum es bei harmonischen Schwingungen geht. Es sind periodische Bewegungen mit konstanter Frequenz. Also wenn wir über einen Ton mit der Frequenz 440 Hz reden, reden wir eigentlich über vielleicht einen Lautsprecher, dessen Membran sich 440 mal in der Sekunde vor und zurück bewegt. Oder im Falle der Stimmgabel, bei der die Zungen exakt das gleiche tun.
Puh, das war anstrengend. Jetzt mach aber eine Pause und dann schau dir einfach nur mal das nächste Bild an.
* = Es gibt ein Gesetz, mit dessen Hilfe man eine Sinuskurve über einen Kreis herleiten kann. Ich hoffe, es stört dich nicht all zu sehr, dass ich solche Dinge ausgelassen habe, da sie für uns wirklich nicht von großer Hilfe sind.
Akustik 1.3
Willkommen zurück beim Audiominds.com Newsletter. Das letzte mal haben wir uns mit Schwingungen beschäftigt, haben aber immer noch keine rechte Ahnung, was wir davon nun haben. Vielleicht klärt sich das so allmählich, wenn wir uns den Wellen zuwenden. Nein, keine Wasserwelle. Auch kein Mikrowellenherd. Warte mal! Es sieht doch glatt so aus, als würde wir auch die Wellen aus dem alltäglichen Leben kennen…
Aha! Jetzt bin ich aber verwirrt. Was sollen unsere alltäglichen Wellen mit Schwingungen zu tun haben? Lies weiter und du wirst es erfahren.
Es ist sehr wichtig zu verstehen, dass Wellen eine Richtung besitzen und ein Medium brauchen, welches sie überträgt. Das trifft allerdings nicht auf Schwingungen zu. Ein solches Medium könnten die Moleküle eines Gases wie Luft oder einer Flüssigkeit wie Wasser sein. Aber nun pass auf: Man kann sich das Medium wie viele kleine, nebeneinander stehende Schwinger vorstellen, die sich gegenseitig beeinflussen. Stell dir eine Reihe Spiralfedern vor. Jede Feder ist über eine Schnur mit ihrem Nachbar verbunden. Würde man also die erste Feder ein wenig anheben, würde ihr die zweite Feder folgen. Genau so:
Akustik 1.4
Lese den nächsten Satz laut und deutlich: Wellen bewegen sich fort und brauchen deshalb ein Medium. Ok, das Medium besteht also aus so einer Art vieler kleiner Schwinger nebeneinander. Genau wie bei den mit einander verbundenen Federn würde das Anheben einer Feder mit leichtem, zeitlichen Verzug auch ihre Nachbarn betreffen.
Dies ist alles vielleicht ein wenig schwer zu verstehen, da es sehr abstrakt ist, aber wenn du es einmal verstanden hast, ist es eigentlich ganz leicht. Wellen bestehen aus keinem Material, so brauchen aber welches, um übertragen zu werden. Zur Veranschaulichung werde ich die Meereswellen heranziehen. Stelle dir Wellen auf einem großen See oder an einem Strand vor. Ganz klar kann man erkennen, wie der Wasserspiegel an einer Stelle ständig steigt und sinkt und man hat den Eindruck, das Wasser würde sich auf einen zu bewegen. Obwohl das zu einem gewissen Grad zutrifft, stellen wir uns die Wellen lieber so vor, als dass sich das Wasser ein vielen Stellen einfach nur auf und ab bewegt. Klar soweit? Wellen können also auch als eine sich fortbewegende Deformierung eines Materials, des Mediums, beschrieben werden.
Schau dir das folgende Schaubild an:
Akustik 1.5
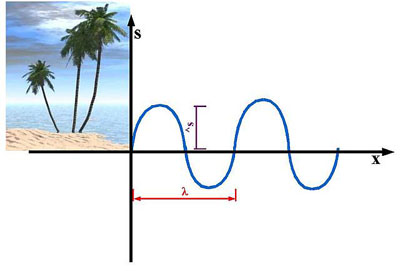
Irgendwie scheint es das selbe Schaubild wie bei den Schwingungen zu sein. Vorsicht ist geboten! Wir sprechen schon längst nicht nur über die Auslenkung zu einer gewissen Zeit. Wir sprechen über die Auslenkung an verschiedenen Orten gleichzeitig. Die x-Achse vertritt dabei die Position. Links des Schaubildes siehst du den imaginären Strand. Die blaue Linie zeigt dabei eine, sich auf den Strand zu bewegende Welle. So langsam ist es an der Zeit, ein paar Definitionen ein zu führen.
Definition: Die Auslenkung eines einzelnen Schwingers nennen wir Amplitude. ^s ("s max") wird dabei die größte Auslenkung oder Amplitude einer Schwingung genannt. s bewegt sich immer zwischen -^s und ^s. l ("Lambda") ist die Wellenlänge.
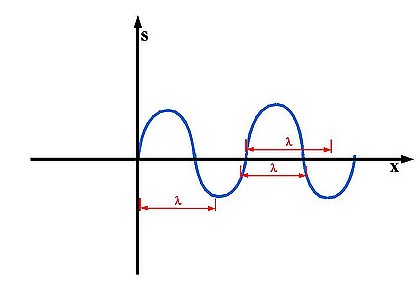
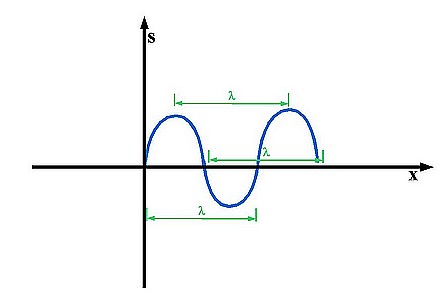
Grafisch betrachtet ist die Wellenlänge der Abstand zwischen zwei Punkten mit der selben y-Position und Richtung (hoch oder runter). Lambda wird üblicher Weiße in Metern gemessen. Einige falsche Lambda kann man in Abbildung 6 sehen:
Akustik 1.6
Und hier ein paar korrekte Wellenlängen:
Akustik 1.7
Ich weiß, dass das alles ziemlich langweiliges und abstraktes Zeugs ist, aber wir sind bald fertig damit - versprochen. Unglücklicher Weiße werden wir es für die nächste Ausgabe benötigen, wenn wir uns der praktischen Anwendung von dem ganzen Kram widmen. Es sei allerdings noch erwähnt, dass wir zwei sehr wichtige Dinge vergessen haben, bevor wir für heute am Ende angelangt sind. Dies seien die Frequenz und die Ausbreitungsgeschwindigkeit einer Welle.
Wiedereinmal gilt: Kann man eine konstante Frequenz einer Welle (Auf und Abs an einer Stelle) bestimmen, ist es eine harmonische Welle. Andernfalls ist es eine unharmonische Welle. (Wer hätts gedacht?) Als eine kleine Daumenregel können wir wieder das Wasser betrachten. Jede Welle beinhaltet viele "Berge" und "Täler". Wenn du mitten im Wasser stehst, ist die Frequenz f die Anzahl der "Berg-Tal"-Paare, die in einer Sekunde an dir vorüber ziehen. Diese Anzahl wird in Hertz (Hz) (benannt nach dem Karlsruher Physiker Heinrich Hertz) oder Umdrehungen pro Sekunde gemessen.
So, dass soll es für heute gewesen sein. Hoffentlich konnten wir beim Editieren, alles richtig stellen. ;-) Nächstes mal werden wir uns der Schallgeschwindigkeit und der Dichte, Elastizität und Dichte der Luft, und wie diese im Zusammenhang stehen, zuwenden.
Bis dahin.
Euer,
Dennis