
Dieser Artikel in deutsch.
[Ed. Note: Dennis Schulmeister is a high school student currently studying in Germany. (As of 2005)]
An audio engineer needs to know at least a little bit about the physics of waves. No matter if doing a live act, setting up mics for an instrument in the studio, or treating a room for good sound, there are some guidelines and rules which when put to good use can make these jobs a lot easier for you.
Sound is composed of waves but before we get into that, let's start out by talking about oscillations. We won't rest long here since most rules of oscillations are of little realworld use for us but let's see how that works for a moment.
There are many oscillators known to us in the real world: Tuning forks, guitar strings, strings in general, amplifier feedback, springs and so on. All those oscillators can be divided into several groups. We divide between harmonic or non-harmonic oscillators and free oscillators or forced oscillators.
So what's a free oscillator? A free oscillator is literally anything that has the ability to vibrate. A free oscillator would be the tuning fork, or the strings and the springs. One example of a forced oscillator is the common loudspeaker. A free oscillator determines it's rhythm of vibration from it's essential makeup. Once activated it contines to oscillate by itself until the energy used to activate it is expended.
A speaker can't oscillate by itself, it would need other inputs (amplifiers mostly). Continuous forces are needed to be sent to the loudspeaker, otherwise it wouldn't do anything. Given its nature, it is capable of many different speeds of oscillation.
Now we have defined free and forced oscillators but what does all that really mean? Unlike guitar strings a tuning fork oscillates very symmetrically. A good tuning fork produces one exact frequency (like 440 Hz). That is because the tines of the tuning fork have the property of Mass, plus they have the property of Elasticity. The position of the tines of the fork before a force is applied is called it's Equilibrium. The amplitude of displacement is proportional to the magnitude of the force applied. That is, the harder we strike the fork, the greater it's magnitude of displacement.
Newton's first law applies: All bodies remain at rest or in a state of uniform motion unless another force acts in opposition. Because of the interaction of the two opposing forces, Elasticity and Inertia, the tines of the fork continue to move to and fro, and the fork is said to have been set into vibration.
Guitar strings have a richer tonality and don't produce a pure tone of one frequency. They are therefore non-harmonic oscillators.
In the area of physics springs are popular oscillators because they oscillate slowly enough to be watched. A little experiment will explain harmonic oscillators further.
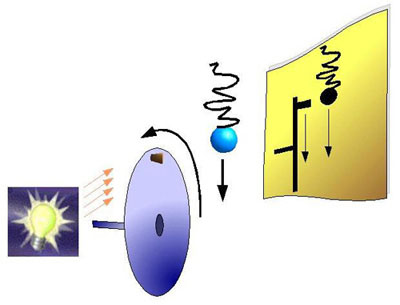
Accoustics 1.1
What we can see on the picture are a light source, a rotating disc with a little cork on it, a spring with a sphere and a paper sheet next to each other. First we pull the spring a bit so that it starts oscillating. Next we try to match the speed of the disc so that both shadows move up and down together. And indeed it IS possible to match the speed of the disc with the spring so that both shadows move in unision.
Some (boring) math and we are able to calculate the spring's position at a given point in time*:
s = ^s * sin(w*t)
with ^s being the maximum position, w being the Angular Velocity and t being the time in seconds. The Angular Velocity w is defined as follows:
w = 2pf
f is the frequency in Hz (movements per second) and p is pi, approx. 3.14159.
So what did we learn? There are different types of oscillations. Free oscillations or forced oscillations and harmonic or non-harmonic oscillations. Unlike forced oscilators free oscillators don't need permanent forces in order to oscillate. Non-harmonic oscillators don't have a fixed frequency and so don't oscillate symmetrically. The position of a harmonic oscillator at a given time t with a given frequency f can be described as
s(f, t) = ^s * sin(2pf * t)
^s is one of the extreme positions. But what does all the math mean to us, you ask? Let me show you another figure. How would the s(f, t) function look when drawn on a coordinate system?
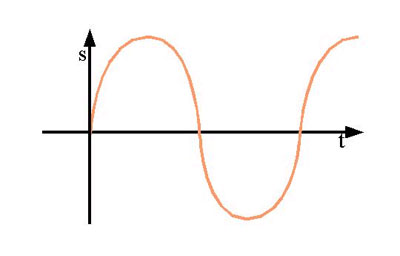
Accoustics 1.2
Remember: The arrow pointing upwards shows the y coordinate. The horizontal arrow shows the x coordinate. The curve is built from many points each being placed by both coordinates.
The x coordinate shows the passage of time in this example. On the y coordinate of one point we can read the corresponding position of the spring (or the sphere on it).
You see the sphere is periodically bumping up and down sometimes faster sometimes slower thus moving very smoothly. And this is what harmonic oscillations are all about. They are periodic and smooth movements with a fixed frequency. So when we're talking about a tone with e.g. 440 Hz all we're talking about is maybe a speaker, the cone of which is moving back and forth 440 times per second, or in the case of our tuning fork, the tines are doing the same thing.
Phew, that was hard. Now have a break and then take a good hard look at the following picture.
* = There's a rule saying that one can calculate a sine curve by using a circle. I hope you don't mind that I left out things like this because they are of no special use for us.

Accoustics 1.3
Welcome back to the Audiominds.com newsletter. Last time we dealt with oscillations but didn't really know what we gained from that experience. Maybe we'll notice when we take a look at the waves. No, not water waves. Not yet. No micro-wave oven. Wait a minute, seems we know waves from real life again… Ahaaa. So, I'm confused. What do waves have to do with oscillations?
It's very important to realize that waves own a direction and need a medium in which to travel, which is untrue for oscillations. Such a medium could be the molecules of a gas like air or a liquid like water. But now take care: One can think of the medium being many oscillators standing next to each other each influencing the next one. Imagine a row of hanging springs. Each spring is connected with its neighbour. So if you raise the first spring the second will follow. Just like this:

Accoustics 1.4
Read out the following sentence loud and clearly: Waves move forward and therefore need a medium. Ok, the medium consists of many little oscillators sitting next to each other. Just like with our connected springs, raising one spring would slightly affect it's neighbors with a time shift also.
This one is a bit hard to understand because it's very abstract but once you get it the rest is very easy. Waves are of no material. They are there when a row of molecules of a medium start to oscillate over time. I'll use the example of water waves in order to make things easier to understand.
Imagine sea waves on a beach. You can clearly see how the water raises and falls periodicly and you have the impression of the water moving towards the beach. While this may be true to a certain point we just think of the water level changing on different spots. Make sense? Waves could also be described as a moving deformation of a given material, the medium.
Look at the following graph:
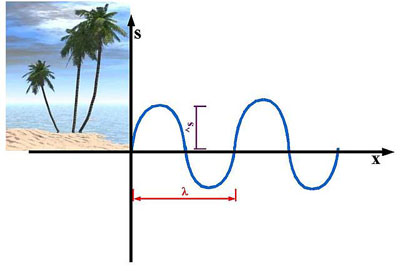
Accoustics 1.5
Seems like the graph looks very similar to the graph of an oscillation. Be careful. We're not talking about differences over a certain time anymore. We're talking about differences at different places now. The x-axis is entitled x which means 'position'. On the left side you see the imaginary beach. The blue line shows one water wave moving towards the beach. Now it's time to introduce some definitions:
Definition: The up-down position of a single (spring-)oscillator is called its amplitude. ^s (read "s max") is called the maximum amplitude of an oscillation or wave. s defines any amplitude between -^s and ^s. l (read "lambda") is called the Wavelength.
When talking about the Wavelength (lambda), the distance between two points on a wave curve with the same y-position (up/down) and the same direction is called the Wavelength. By the same direction I mean whether the curve is moving upwards or downwards. Lambda is measured in meters. Some examples of wrong Lambdas or Wavelengths can be seen in figure 6:
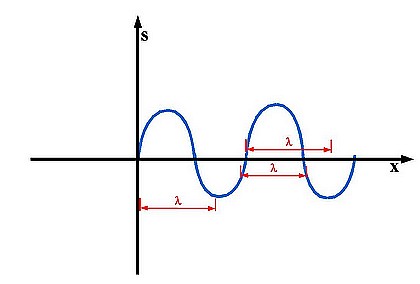
Accoustics 1.6
And here some correct wave lengths:
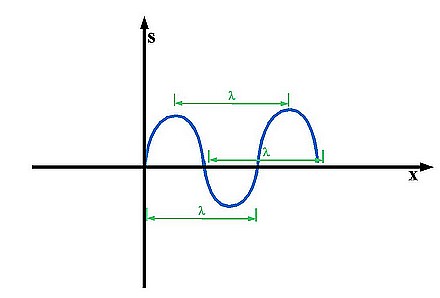
Accoustics 1.7
I know this is some boring abstract stuff, but it's soon finished. Unfortunatly we'll need it for the next issue when we deal with the practical use of all that jazz, but it must be said that we are still missing two very important things before we're done for now, and those are the frequency and the speed of a wave.
Again, if you're able to determine an exact single fundamental frequency for a wave it is a harmonic wave. Otherwise it's a non-harmonic wave. As a simple rule of thumb you could use the water example here again. Each wave contains many 'mountains' and 'valleys'. If you stand in the middle of the sea the frequency f is the amount of 'mountain'-'valley' couples passing you during one second. They are meassured in Hertz (Hz) or cycles/sec, named after the German physicist Heinrich Hertz.
That's all for this installment. Hopefully we got everything right in the editing. Next time, we'll take a look at issues having to do with the speed of sound, the density, elasticity and temperature of the air, and how they relate to each other within the scope of our endeavors.
Yours,
Elwood